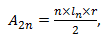Matemática hindu

Contexto Histórico


Escavações arqueológicas ocorridas em Mohenjo Daro nos dão uma indicação de uma civilização muito antiga e de uma cultura muito alta na Índia, ocorrida na mesma época em que eram construídas as pirâmides no Egito. Posteriormente o país foi ocupado pelos invasores arianos que impuseram o sistema de castas, o qual trouxe um atraso muito grande ao desenvolvimento. Estes invasores arianos desenvolveram na índia a literatura sânscrita. Na mesma época em que Pitágoras começou a desenvolver seus teoremas e axiomas na Grécia, Buda agia na Índia. Especula-se que Pitágoras esteve em contato com Buda e que desenvolveu seu mais famoso teorema com os hindus.
Os indianos dos primeiros tempos foram exterminados por volta de 1500 ac. Este país tinha como política, vários pequenos principados desunidos, o que propiciou muitas invasões em seu território (arianas, persas, gregas, árabes e ingleses). Estes invasores se estabeleceram como classe dominante, evitando a miscigenação com o povo nativo.
Entre 3000 ac e 1500 ac viveu na índia um povo, da região do rio Indo, que cultivava a agricultura e morava em cidades. Este povo foi destruído pelos arianos. Entre 1500 ac e 500 ac os arianos desenvolveram o hinduismo, combinação de religião, filosofia e estrutura social, a qual veio a desenvolver a base de sua civilização. O hinduismo é um conjunto de crenças e leis que se baseia em três idéias principais: culto a um grande número de deuses, transmigração da alma e o sistema de castas que dividia rigidamente a sociedade indiana em quatro classes: Brahmana (sacerdotes), kshatriya (guerreiros), vaisya (comerciantes e artesãos) e sudra (camponeses).


Contexto Matemático 


A matemática hindu apresenta mais problemas históricos do que a grega, pois os matemáticos indianos raramente se referiam a seus predecessores e exibiam surpreendente independência em seu trabalho matemático.
A Índia, assim como o Egito, tinha seus “esticadores de corda”. As primitivas noções geométricas tomaram corpo no escrito conhecido como “Sulvasutras” (regras de cordas). Este escrito tem três versões, sendo que a mais conhecida tem o nome de Apastamba. Nesta primeira versão, da mesma época de Pitágoras, são encontradas regras para construção de ângulos retos por meio de ternas de cordas cujos comprimentos formam tríadas pitagóricas. Este escrito, provavelmente, sofreu influência babilônica, visto que estas tríadas encontram-se nas tábuas cuneiformes. A origem e a data dos Sulvasutras são incertos, de modo que não é possível relacioná-los com a primitiva agrimensura egípcia ou com o problema grego de duplicar um altar.
Após esta publicação, surgiram os “Siddhantas” (sistemas de astronomia). O começo da dinastia Gupta (290) assinalou um renascimento da cultura sânscrita e estes escritos podem ter sido um produto disto. A trigonometria de Ptolomeu se baseava na relação funcional entre as cordas de um círculo e os ângulos centrais que subentendem. Para os autores dos Siddhantas, a relação ocorre entre metade de uma corda de um círculo e metade do ângulo subentendido no centro pela corda toda.

A Índia teve muitos matemáticos que fizeram grandes contribuições. Entre eles podemos destacar:


Aryabhata

Publicou, em 499, uma obra intitulada “Aryabhatiya”. Esta publicação é um pequeno volume sobre astronomia e matemática, semelhante aos “Elementos” de Euclides, porém de oito séculos antes. São compilações de resultados anteriores. Esta obra contém: nome das potências de dez, até a décima; regras de mensuração (muitas erradas); área do triângulo; volume da pirâmide (incorreto); área do círculo; volume da esfera (incorreto) e áreas de quadriláteros (algumas incorretas). Também encontramos cálculos com a medida do tempo e trigonometria esférica.

Brahmagupta

 Viveu na Índia central pouco mais de cem anos depois de Aryabhata. Tem pouco em comum com seu predecessor que vivia no leste da Índia. Seu trabalho mais importante foi a generalização da fórmula de Heron para achar a área de qualquer quadrilátero. Também trabalhou na solução de equações quadráticas com raízes negativas.

Bhaskara

Considerado o mais importante matemático do século doze (1114 – 1185). Ele preencheu as lacunas do trabalho de Brahmagupta. É dele a primeira resposta plausível para a divisão por zero. Em seu trabalho “Vija-Ganita” ele afirma que tal quociente é infinito. Sua outra obra, “Lilavati”, apresenta tópicos sobre equações lineares e quadráticas, determinadas e indeterminadas, mensuração, progressões aritméticas e geométricas, radicais, tríadas pitagóricas, entre outras. Sua obra representa a culminação de contribuições hindus anteriores.

Ramanujan

Após Bhaskara, a Índia passou vários séculos sem matemáticos de importância comparável. Srinivasa Ramanujan (1887-1920) é considerado o gênio hindu, em aritmética e álgebra, do século vinte.
A introdução de uma notação para uma posição vazia, o símbolo para o zero, foi o segundo passo para o nosso moderno sistema de numeração. Não se sabe se o número zero (diferente do símbolo para a posição vazia) surgiu junto com os nove numerais hindus. É bem possível que o zero seja originário do mundo Grego, talvez de Alexandria. Possivelmente foi transmitido à Índia depois que o sistema posicional já estava estabelecido lá. É interessante observar que os Maias do Yucatán (México), anterior à Colombo, usavam notação posicional, com notação para a “posição vazia”. Com a introdução, na notação hindu, do décimo numeral, um ovo de ganso para o zero, o nosso moderno sistema de numeração para os inteiros estava completo.


A nova numeração, geralmente chamada de hindu-arábica, é uma nova combinação dos três princípios básicos, todos de origem antiga:


i) base decimal
ii) notação posicional
iii) forma cifrada para cada um dos dez numerais


Nenhum destes de se deveu, originalmente, aos hindus, mas foi devido a eles que os três foram ligados pela primeira vez para formar o nosso sistema de numeração.
Outra contribuição importante dos hindus foi a introdução de um equivalente da função seno na trigonometria para substituir a tabela de cordas dos gregos. A trigonometria hindu era um instrumento útil e preciso para a astronomia.

Aplicações matemáticas

Vários documentos arqueológicos indicam que os algarismos (de Al Khwarism) é indo – arábico, ou seja, teve sua origem no Norte da Índia cerca de 500 d.C. e foi levada pelos árabes durante sua invasão e expansão por toda Europa.

Os antigos hindus já usavam uma forma de algarismos semelhante desde cerca de 300 a.C. Esta numeração já tinha uma característica do sistema moderno. Seus nove primeiros algarismos eram sinais independentes:

  

o que significava que um número como o 5 não era entendido como 5 unidades mas como um símbolo independente.

Ainda existia naquela época a dificuldade posicional e os hindus passaram a usar a notação por extenso para os números, pois não conseguiam exprimir grandes números por algarismos.

Cada algarismo tinha um nome:

Contrariamente à nossa numeração oral atual, (em que os números 10 000, 100 000, 10 000 000, por exemplo são denominados, respectivamente, dez mil, cem mil e dez milhões em que os nomes do milhar e do milhão desempenham o papel das bases auxiliares), o sistema falado pelos sábios hindus não privilegiavam nenhum número. Ele atribuía às diferentes potências de dez nomes independentes uns dos outros:

10            = dasa

100           = sata

1.000         = sahasra

10.000        = ayuta

100.000       = laksa

1.000.000     = prayuta

10.000.000    = koti

100.000.000   = vyarbuda

1.000.000.000 = padma

Ao invés de fazer como hoje, de acordo com as potências decrescentes de 10, os hindus escreviam os números em ordem crescente das potências de 10 por volta do século IV d.C. Eles começavam pelas unidades, depois pelas dezenas, pelas centenas e assim por diante. O número 4602 era representado por:

Poderíamos escrever o número 12.345 como

pañca caturdasa trisata dvisahasra ayuta

pois, 12.345 = 5 + 40 + 300 + 2.000 + 10.000, logo:

5      = pañca

40     = catur dasa

300    = tri sata

2.000  = dvi sahasra

10.000 = ayuta

pañca caturdasa trisata dvisahasra ayuta

Esta já era uma forma especial.

Em virtude da grande repetição que ocorria com as potências de 10, por volta do século V d.C, os matemáticos e astrônomos hindus resolveram abreviar a notação retirando os múltiplos de 10 que apareciam nos números grandes, assim o número 12.345 que era escrito como:

pañca caturdasa trisata dvisahasra ayuta

12345 = 5 + 4×10 + 3×100 + 2×1000 + 1×10000

E esta se transformou em uma notação falada e escrita posicional excelente para a época.

Porém começaram a acontecer alguns problemas como escrever os números 321.

O número 321 é facilmente representado por:

“Um. Dois. Três”

321 = dasa dvi tri

321 = 1 + 2 x 10 + 3 x 100

Mas há, por outro lado, uma grande dificuldade para exprimir um número como 301, onde falta um decimal. Não basta dizer:

 “Um. Três”  que corresponde a 31. O que não é 301. Há uma lacuna. È necessário uma palavra que signifique que não há dezena. Quando se aplica rigorosamente o princípio de posição aos nomes das nove unidades simples, faz-se necessário o uso de um vocábulo especial para marcar a ausência das unidades. Os sábios criaram a palavra “sunia”, que significa vazio, logo 301 passa a ser escrito como:

“Eka. Sunia. Tri”

“Um. Vazio. Três”

Assim, não há mais equívocos. Depois dos babilônios e à mesma época que os maias, os hindus  inventaram o zero. A partir desse momento todos os aspectos convergiram para a consolidação do sistema numérico que conhecemos hoje. Os sábios hindus dispunham agora de unidades distintas de 1 a 9, já conheciam o princípio da posição, e acabavam de inventar o zero.

O documento mais velho dos hindus foi escrito por Aricabata em meados de 500 a.C, e era chamado  Suriasidanta. Esse é tido como primeiro estudo trigonométrico na Índia, nele Ariabata calculava o seno (chamado de jivas) dos ângulos pertencentes ao primeiro quadrante de um circulo o qual o raio era de 3.438, que dividia-se em 21.600 graus, ( ou seja os hindus subdividiam os graus gregos em 60 partes).

Para calcular os senos que eram superior a 30^o (1.800^o)  Ariabata utilizara o mesmo processo que Ptolomeu, mas para os ângulos menores que 30⁰ que ele dizia “numericamente igual à quantidade de partes em que foi dividida a circunferência”.

                                                             lim sen x _{x -- 0} =  x 

                                                        primeiro limite fundamental

Ariabata, também  representa  no Suriasiadanta, o valor de pi como sendo 124.764 dividido por 40.000, (3,119).

Divisão e Multiplicação

Em 620  Brahmagupta escreve o Sidhanta ( “calculo” escrito em couro),   o principal achado desse trabalho são os algoritmos da multiplicação e da divisão, ( que segundo ele os indus aviam descobertos desde 100 a 200 d.C).

            Divisão exemplo

Processo multiplicativo 

       

 

Esse processo de multiplicação consta de se multiplicar cada algarismo, depois soma-se as diagonais:  21 x 14 = 294

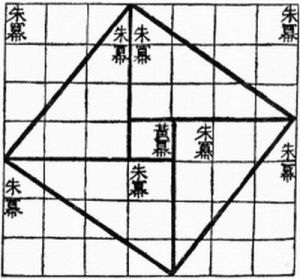
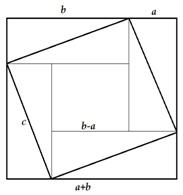
Brahmagupta também discorre sobre uma regra de construção das tríades pitagóricas:

“...é fácil, oh querido aluno, encontrar os números que satisfazem o triangulo  divino ( retângulo). Basta seguir as instruções do seu venerado mestre: pegue um dos números 2,3,4, 5, etc. E multiplique por 2, em seguida, subtraia 1. Teremos o primeiro lado. Para o segundo faça...”.

vejamos como uma representação:

Pesquisa apresentada pelos discentes da FAINTVISA, durante vivencia da Disciplina História da Matemática (Licenciatura em Matemática): Adonias Kadús de Sousa, Adriana Maria de santana e Sandra Alves de Carvalho.

Matemática na China

Na China, a matemática era vista como uma necessidade e utilidade. Era importante educar e construir um país com grande desenvolvimento, sendo a Arquitetura, o Comércio, as Financias e a Agrimensura as bases para este crescimento. Os chineses tinham um método para resolver sistema de equações lineares muito semelhante ao «Método de Gauss»; começaram a usar o número negativo mais cedo que todas as outras civilizações; no séc. V usavam 355/113  para π, valor atribuído a um matemático Métius no séc. XVI; pelo séc. VII já calculavam o volume da esfera usando o Princípio de Cavalieri (séc. XVII); No séc. XII, Yang Hui provou a fórmula que determina “a soma dos quadrados dos n primeiros números naturais por reunião de volumes”, a mesma descoberta surgiu no ocidente no 19.º século. O facto da matemática chinesa ter-se desenvolvido durante 3 milênios originou uma infinidade de aspetos com teor matemático, contudo nesta secção iremos destacar aqueles que entendemos serem os mais importantes.

Sistema numérico

       Os chineses foram umas das primeiras civilizações a entender que os cálculos num sistema decimal são mais simples e eficazes. Em 1500 anos a.C. tinham sistema com 5000 caracteres posicionais, mais tarde inventaram os cilindros de contagem. No séc. V a. C. já se efetuavam as quatro operações aritméticas recorrendo aos cilindros. Estes tinham duas cores, uma para representar os positivos, outra para representar os negativos.

        O sistema é bastante útil e prático, contudo tem as suas desvantagens, pois a verificação dos cálculos podia ser exaustiva e o trabalho com vários cilindros podia ser demorado. As operações são muito semelhantes às nossas, com a diferença de se realizarem da esquerda para a direita e de se considerar o algarismo de maior ordem na multiplicação.

Nove Capítulos sobre a arte da Matemática

      Antes do aparecimento da maior obra chinesa “Nove Capítulos sobre a arte da Matemática”, o povo chinês já tinha um raciocínio matemático avançado. No campo da Lógica eram discutidos e estudados paradoxos muito semelhantes aos de Zenão (séc. V a.C.), mas a área de maior interesse era a astronomia. Neste século surgiu um dos teoremas chineses mais conhecidos, o Teorema de Kou Ku/Gougu. Com o passar dos séculos, foram construídos manuais escolares com noções do campo da astronomia, da arquitetura, da engenharia, da aritmética e da geometria.

          Liu Hui (250 anos a.C.), um dos maiores matemáticos chineses, considerado o Euclides Chinês, fez comentários à obra Nove Capítulos sobre a arte da Matemática e reescreveu-a com alguns melhoramentos. Possivelmente, a obra original foi escrita antes de 400 anos a.C. e era constituída por uma mistura de conhecimentos de diferentes autores. A obra de Liu Hui está dividida em 9 capítulos, sendo o 1.º Capítulo sobre a Medição de Campos.

1.º Capítulo

Este capítulo indica o processo simplificar, somar/subtrair e multiplicar/dividir frações. No caso da simplificação de frações, eles utilizavam o máximo divisor comum (m.d.c) usando subtrações sucessivas dos restos. Para somar ou subtrair eles colocavam todas as frações com o mesmo denominador fazendo o mínimo múltiplo comum (m.m.c.). Para multiplicar ou dividir calculavam o m.d.c. e procediam como nos dias de hoje. O mesmo tratamento nas operações com frações foi utilizado no século VII na India e no século XV na Europa. Ainda neste capítulo, Liu Hui dá uma aproximação de π baseada no limite, “se escrever um polígono de n lados, com n o maior número possível de lados, dentro de um círculo, então a área do círculo é igual à área do polígono”. Hui conseguiu mostrar que π=3,141024 , substituindo n por 192 na fórmula

onde ln  representa o comprimento do lado do polígono regular de n lados, r o raio de um circulo de comprimento 1 pé chinês e  a área do polígono regular de A_2n lados. Zu Chongzhi, 200 anos depois, enquadrou π entre 3,1415926 e 3,1415927. Este melhoramento foi alcançado mil anos mais tarde na Europa.

Do 2.º Capitulo ao 6º Capitulo

Nestes capítulos são ensinadas as regras das proporções, o método da falsa posição ou regra três simples, o método da decomposição ou dissecação de uma figura para usar nos sólidos geométricos.

7.º e 8º Capítulos

        No 7º e 8º capítulo surgem as equações indeterminadas, as equações com várias incógnitas, a regra da dupla falsa posição, mais tarde aplicada pelos Árabes na Idade Média e por Fibonacci (séc. XIII), e o modo de operar com números negativos usando os cilindros de contagem. Esta visão e o conceito de operar foi utilizada na India, no séc. VII e na Europa, no séc. XVI. Uma equação com duas incógnitas era resolvida por um processo idêntico ao da regra de Cramer, ou seja, calculando o determinante de uma matriz. O cálculo de determinantes foi usado pelo japonês Seki Kowa e 10 anos mais tarde por Leibniz em 1693. O Método das tabelas era usado na resolução de equações com várias incógnitas na forma matricial e consiste na combinação linear de colunas para eliminar alguns elementos da equação e obter a solução. Esta invenção chinesa foi também descoberta pelo francês Buteo, em 1500.

9.º Capitulo

         No último capítulo são apresentados problemas envolvendo triângulos retângulos através de dois conceitos, “empilhar quadrados” e a função tangente. Hui pressagiou a utilização das razões trigonométricas e mostrou como resolver equações do 2ºgrau usando um método semelhante ao do babilónico.

          Este manual foi criado por Liu Hui no séc. VII e contém o método das diferenças duplas (criado entre 206 a.C. e 24 d.C.) que é utilizado no cálculo de distâncias usando a diferença entre duas observações. O primeiro problema envolve a altura de uma ilha (x)  e a sua distância ao primeiro poste (y)  como mostra a ilustração 11. Da figura são conhecidas as alturas dos dois postes (h) , a distância entre eles(d) , a distância entre o 1º poste e a posição que se tem que recuar para ver o topo da ilha (a₁) e a distância entre o 2º poste e a posição que se tem que recuar para ver o topo da ilha (a₂) .

Usando estes dados, Liu Hui aplicou o método das diferenças duplas e descobriu as seguintes fórmulas:

          Este método foi usado noutros problemas, nomeadamente na topografia, para medir a “altura do Sol”. Este processo mostra a tentativa da inclusão da Álgebra na China, contudo só aconteceu no séc. XIII.

Chao Chung Ching e o comentário ao Teorema de Gougu

“O imperador Yu domina inundações, aprofunda rios e correntes, observa a forma das montanhas e vales, contempla lugares altos e baixos, alivia as maiores calamidades e salva as pessoas do perigo […]. Isto é possível pelo Teorema de Gougu”.

        Este teorema originou 21 teoremas com ilustrações, infelizmente quase todos foram perdidos. O “diagrama sobre a hipotenusa é um dos sobreviventes (Ilustração seguinte).

       

              

       Chao Ching conseguiu deduzir uma fórmula interessante para os catetos a e b , usando a hipotenusa, a adição e a subtração entre a e b , com a < b. Observando o diagrama podemos afirmar que a área do quadrado exterior, de lado a + b , é igual à adição da área do quadrado de lado c  com a área de 4 triângulos de catetos a e b , ou seja,

Fórmulas semelhantes a estas eram aplicadas constantemente pela civilização Babilónica no cálculo de áreas.

Nove Secções da Arte dos Números e a Teoria Dos Números

         Sun Tsu, 100 anos d. C. escreveu um manual de matemática, composto por três livros, onde definiu medidas para o comprimento, área e volume, para o peso de vários objetos; utilizou métodos iguais aos de hoje para somar duas frações (regra da cruz); descreveu um algoritmo para obter a raiz quadrada e construiu um calendário que levantou alguns problemas relacionados com a congruência de números, o que o levou à criação de um dos mais famosos teoremas na Teoria dos Números, o Teorema Chinês dos Restos.

           Mais tarde, Ch’in Chiu-Shao cria a obra Nove Secções da Arte dos Números (em 1247) que consistiu num melhoramento das obrasNove Capítulos e no Manual da Ilha do Mar. A obra apresenta problemas que envolvem o cálculo de figuras geométricas reais; problemas que envolvem uma fórmula semelhante à de Herão para calcular a área de figuras; problemas de trigonometria; contém progressões aritméticas/geométricas, equações de grau superior a dois que envolvem o método de Horner ou Regra de Ruffini; mas as suas maiores inovações aparecem na resolução de equações determinadas, usando o método do elemento celestial e na resolução de equações indeterminadas onde descreve detalhadamente o método chinês. Seguidamente vai ser exposto o método chinês utilizado num dos 81 problemas da sua obra.

 

        Teoria dos Números também foi estudada por Diofanto de Alexandria (275 anos d.C.), por Fibonacci (1202 anos d.C.) e atingiu o apogeu com Euler (em 1801) e Gauss (em 1801).

Comentário de Yang Hui à obra Nove Capítulos

Método de Yang Hui

Anéis, formas, dragões e tartarugas

     Todas as civilizações, para se divertirem e ocuparem o tempo, tinham vários jogos e passatempos, que utilizavam a matemática. Na China, existiam vários puzzles, um deles era os nove anéis ligados, que consistia na separação de nove anéis todos ligados entre si. Para resolver este puzzle era necessário saber um pouco sobre números binários.

      Outro puzzle que envolvia formas geométricas é o famoso Tangram. O yizhitu é uma variante do Tangram e contém 15 peças. Este puzzle tem uma grande utilidade pois ensina relações importantes entre as áreas de figuras planas.

       Uma famosa lenda chinesa diz que o imperador Yu tinha na sua posse dois diagramas muito especiais. Estes foram trazidos até ele por dois animais, um dragão-cavalo (Ho Thu) e uma tartaruga (Lo shu). Nas costas de ambos encontravam-se os desenhos da ilustração 13 e como podemos ver, um deles trata-se de um quadrado mágico 3 por 3 onde a soma dá 15. Os chineses tinham um grande fascínio por quadrados mágicos, estes quadrados foram primeiramente observados por árabes mas é aos chineses que se deve a construção da teoria sobre quadrados mágicos.

Pesquisa apresentada pelos discentes da FAINTVISA, durante vivencia da Disciplina História da Matemática (Licenciatura em Matemática): Alydiane Felix, Deyvison de Alcantara, Everton Cardoso e Luiz Severino.