Proporção áurea
Proporção áurea, número de ouro, número áureo, secção áurea, proporção de ouro é uma constante real algébricairracional denotada pela letra grega  (PHI), em homenagem ao escultor Phideas (Fídias), que a teria utilizado para conceber o Parthenon, e com o valor arredondado a três casas decimais de 1,618. Também é chamada de se(c)ção áurea (do latim sectio aurea) , razão áurea, razão de ouro, média e extrema razão (Euclides), divina proporção,divina seção (do latim sectio divina), proporção em extrema razão , divisão de extrema razão ou áurea excelência. O número de ouro é ainda frequentemente chamado razão de Phidias .
(PHI), em homenagem ao escultor Phideas (Fídias), que a teria utilizado para conceber o Parthenon, e com o valor arredondado a três casas decimais de 1,618. Também é chamada de se(c)ção áurea (do latim sectio aurea) , razão áurea, razão de ouro, média e extrema razão (Euclides), divina proporção,divina seção (do latim sectio divina), proporção em extrema razão , divisão de extrema razão ou áurea excelência. O número de ouro é ainda frequentemente chamado razão de Phidias .
 (PHI), em homenagem ao escultor Phideas (Fídias), que a teria utilizado para conceber o Parthenon, e com o valor arredondado a três casas decimais de 1,618. Também é chamada de se(c)ção áurea (do latim sectio aurea) , razão áurea, razão de ouro, média e extrema razão (Euclides), divina proporção,divina seção (do latim sectio divina), proporção em extrema razão , divisão de extrema razão ou áurea excelência. O número de ouro é ainda frequentemente chamado razão de Phidias .
(PHI), em homenagem ao escultor Phideas (Fídias), que a teria utilizado para conceber o Parthenon, e com o valor arredondado a três casas decimais de 1,618. Também é chamada de se(c)ção áurea (do latim sectio aurea) , razão áurea, razão de ouro, média e extrema razão (Euclides), divina proporção,divina seção (do latim sectio divina), proporção em extrema razão , divisão de extrema razão ou áurea excelência. O número de ouro é ainda frequentemente chamado razão de Phidias .
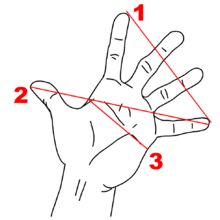
Desde a Antiguidade, a proporção áurea é usada na arte. É frequente a sua utilização em pinturas renascentistas, como as do mestre Giotto. Este número está envolvido com a natureza do crescimento. Phi (não confundir com o númeroPi  ), como é chamado o número de ouro, pode ser encontrado de forma aproximada no homem (o tamanho dasfalanges, ossos dos dedos, por exemplo), nas colmeias, entre inúmeros outros exemplos que envolvem a ordem de crescimento na natureza.
), como é chamado o número de ouro, pode ser encontrado de forma aproximada no homem (o tamanho dasfalanges, ossos dos dedos, por exemplo), nas colmeias, entre inúmeros outros exemplos que envolvem a ordem de crescimento na natureza.
 ), como é chamado o número de ouro, pode ser encontrado de forma aproximada no homem (o tamanho dasfalanges, ossos dos dedos, por exemplo), nas colmeias, entre inúmeros outros exemplos que envolvem a ordem de crescimento na natureza.
), como é chamado o número de ouro, pode ser encontrado de forma aproximada no homem (o tamanho dasfalanges, ossos dos dedos, por exemplo), nas colmeias, entre inúmeros outros exemplos que envolvem a ordem de crescimento na natureza.
Justamente por ser encontrado em estudos de crescimento o número de ouro ganhou um status de "ideal", sendo alvo de pesquisadores, artistas e escritores. O fato de ser apoiado pela matemática é que o torna fascinante.
Definição algébrica
A razão áurea é definida algebricamente como:
A equação da direita mostra que  o que pode ser substituído na parte esquerda, resultando em:
o que pode ser substituído na parte esquerda, resultando em:
 o que pode ser substituído na parte esquerda, resultando em:
o que pode ser substituído na parte esquerda, resultando em:
Cancelando b em ambos os lados, temos:
Multiplicando ambos os lados por  resulta:
resulta:
 resulta:
resulta:
Finalmente, subtraindo 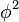 de ambos os membros da equação e multiplicando todas as parcelas por
de ambos os membros da equação e multiplicando todas as parcelas por  encontramos:
encontramos:
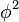 de ambos os membros da equação e multiplicando todas as parcelas por
de ambos os membros da equação e multiplicando todas as parcelas por  encontramos:
encontramos: que é uma equação quadrática da forma
que é uma equação quadrática da forma 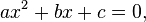 em que
em que 
Agora, basta resolver essa equação quadrática. Pela Fórmula de Bháskara:




A única solução positiva dessa equação quadrática é a seguinte:
 que é o número
que é o número 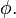
Figuras geométricas
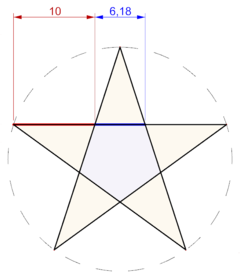
Um decágono regular, inscrito numa circunferência, tem os lados em proporção áurea com o raio da circunferência.Um pentagrama regular é obtido traçando-se as diagonais de um pentágono regular. O pentágono menor, formado pelas interseções das diagonais, também está em proporção com o pentágono maior, de onde se originou o pentagrama. A razão entre as medidas dos lados dos dois pentágonos é igual ao quadrado da razão áurea. A razão entre as medidas das áreas dos dois pentágonos é igual a quarta potência da razão áurea.Chamando os vértices de um pentagrama de A, B, C, D e E, o triângulo isósceles formado por A, C e D tem seus lados em relação dourada com a base, e o triângulo isósceles A, B e C tem sua base em relação dourada com os lados.Quando Pitágoras descobriu que as proporções no pentagrama eram a proporção áurea, tornou esse símbolo estrelado como a representação da Irmandade Pitagórica. Esse era um dos motivos que levava Pitágoras a dizer que "tudo é número", ou seja, que anatureza segue padrões matemáticos.Vegetais
Como os vegetais não têm formas exatas, a ponto de serem construídos com régua e compasso, a divina proporção, bem como a série Fibonacci, só podem ser encontradas por aproximação.Animais
Nos animais, as medidas também são aproximadas.- População de abelhas – A proporção entre abelhas fêmeas e machos em qualquer colmeia.
- Concha do caramujo Nautilus – A proporção em que cresce o raio do interior da concha desta espécie de caramujo. Estemolusco bombeia gás para dentro de sua concha repleta de câmaras para poder regular a profundidade de sua flutuação. Obs.: até hoje não se encontrou nenhum caramujo Nautilus que comprove essa afirmação amplamente difundida.
- Outros – phi estão também nas escamas de peixes, presas de elefantes, crescimento de plantas.
Corpo humano
- A altura do corpo humano e a medida do umbigo até o chão.
- A altura do crânio e a medida da mandíbula até o alto da cabeça.
- A medida da cintura até a cabeça e o tamanho do tórax.
- A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.
- O tamanho dos dedos e a medida da dobra central até a ponta.
- A medida da dobra central até a ponta dividido e da segunda dobra até a ponta.
Essas proporções anatômicas ideais foram representadas pelo "Homem Vitruviano", obra deLeonardo Da Vinci.- Dimensão do útero em mulheres jovens (16 e 20 anos), segundo o pesquisador Jasper Vergtus, da Universidade de Leuven.
Aplicações
O homem, em muitas ocasiões, tem buscado o ideal da perfeição nas linguagens artísticas.Arte
A proporção áurea foi muito usada na arte, em obras como O Nascimento de Vênus, quadro de Botticelli, em que Afrodite está na proporção áurea. Essa proporção estaria ali aplicada pelo motivo de o autor representar a perfeição da beleza.Em O Sacramento da Última Ceia, de Salvador Dalí, as dimensões do quadro (aproximadamente 270 cm × 167 cm) estão numa Razão Áurea entre si. Na história da arte renascentista, a perfeição da beleza em quadros foi bastante explorada com base nessa constante. Vários pintores e escultores lançaram mão das possibilidades que a proporção lhes dava para retratar a realidade com mais perfeição.A Mona Lisa, de Leonardo da Vinci, tem a proporção áurea nas relações entre o tronco e a cabeça, bem como nos elementos da face, mas isso é uma característica inerente ao ser humano e tais proporções podem ser encontradas na maioria das pinturas em que a anatomia tenha sido respeitada. Medições feitas por computador mostraram que os olhos de Mona Lisa estão situados em subdivisões áureas da tela.Retângulo dourado
Em geometria, o retângulo de ouro surge do processo de divisão em média e extrema razão, de Euclides. Ele é assim chamado porque ao dividir-se a base desse retângulo pela sua altura, obtêm-se o número de ouro 1,618.Música
O número de ouro está presente em diversas obras de compositores clássicos, sendo o exemplo mais notável a famosa sinfonia n.º 5, deLudwig van Beethoven . O compositor húngaro Béla Bartók também se utilizou desta relação de proporcionalidade constantemente em sua obra , assim como o fez o francês Claude Debussy em diversas de suas sonatas .Literatura
No livro "O Número de Ouro", Matila Ghyka demonstrou a existência da proporção áurea em textos escritos por Victor Hugo, Shakespeare, Paul Valéry, Pierre Louys, entre outros. Na pesquisa Ghyka relacionou as estrofes de acordo com o ritmo da leitura, o que ele chamou de ritmo prosódico.[21]Cinema
O diretor russo Sergei Eisenstein se utilizou do número no filme O Encouraçado Potemkin para marcar os inícios de cenas importantes da trama, medindo a razão pelo tamanho das fitas de película.
no filme O Encouraçado Potemkin para marcar os inícios de cenas importantes da trama, medindo a razão pelo tamanho das fitas de película.- Referência Bibliográfica
- https://pt.wikipedia.org/wiki/Proporção_áurea. acessado em 27/11/2015.










Junto com a Proporção Áurea e a Arte Grega, a Civilização Ocidental é inteiramente fundamentada na Beleza Americana, na Estética Italiana, na Elegância Francesa e na Cultura Inglesa também.
ResponderExcluir